צורה תלת ממדית מושלמת מאת אלכסנדר צ'רקוב, מתוך ספר המבוא לעולם האמנות "פיסול, ציור, רישום ולא רק"
את החלק הזה אני מדגים באופן מלא עם תצלומי עבודותיו של אניש קאפור, כביטוי של הכרת תודה לאמן שהרשים אותי.
בהיותי נער, יצא לי להשתתף באולימפיאדה בפיזיקה בין תלמידי בתי הספר. אחת השאלות הייתה: "איזו צורה יש למים?". כמו רוב המשתתפים, אני השבתי שלמים יש צורה של כלי אליו הם נמזגים. הסתבר שטעיתי. אחרי האולימפיאדה, המורה לפיזיקה הסביר כי למים במצב חופשי יש צורה של כדור, שכן כך היחס בין פני השטח לנפח הוא מינימלי. נזכרתי בכך כשראיתי לראשונה את יצירות הפיסול של אניש קאפור.
מאפייני הקומפוזיציה הפיסולית: צורה תלת ממדית מושלמת
בטבע, כל מה שנמצא במצב חופשי נוטה לצורה של כדור. החל מערפיליות קוסמיות, כוכבים וכוכבי לכת ועד לאטומים ואלקטרונים. באחד משיריו של המשורר הרוסי של המאה העשרים, ארסני טרקובסקי (אביו של הבמאי הגדול אנדריי טרקובסקי) יש שורה כזו: "חלל עולמי כדורי".
ומה עם הצורות הגיאומטריות האחרות?
במישור קיימים מצולעים רבים – משולש, מרובע, מחומש וכן הלאה. מעגל – ניתן גם כן להציג בתור מצולע, אשר אצלו מספר הזוויות שואף לאינסוף. בתלת ממד, המקבילות שלהם הם הפוליאתרונים, וכדור מהווה צורה תלת ממדית בעלת מספר אינסופי של פאות.
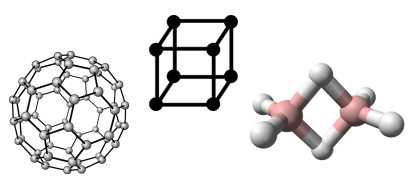
צורות עם מספר מוגבל של זוויות ופאות משמשות כסכמות רבות חיבורים של צורות כדוריות (כמו למשל, אטומים ומולקולות).
בשובנו לפסל של אניש קאפור, אינני יכול שלא להביע את תדהמתי מהאמן, שפסלו הווירטואוזי מאפשר לנו לראות באמצעות צורה בסיסית אחת בלבד – את עולם של פיסול מופשט אשר נבנה כדור. וריאציות מרובות של כדורים בגדלים, מיקומים, צבעים ומרקמים שונים יוצרים תמונה אמנותית ופילוסופית של היקום הסובב אותנו.
מוצרי פיסול
-
- אזל המלאי
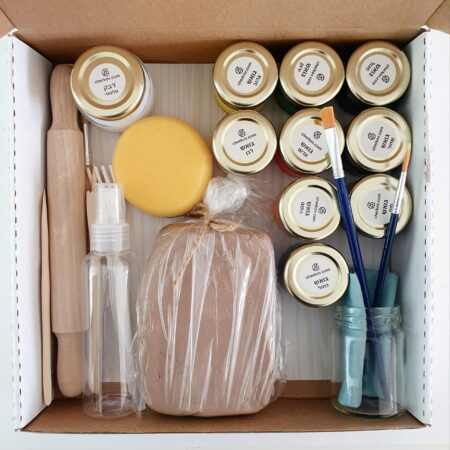
קיט פיסול חמר לילדים
- ₪100
- קרא עוד
-